СОЛИТОНЫ В КАРТИНЕ ТЕПЛОВОГО РАВНОВЕСИЯ НЕЛИНЕЙНЫХ ЦЕПОЧЕК

К.ф.-м.н. Еремейченкова Ю.В., к.ф.-м.н. Метлов Л.С., д.т.н. Морозов А.Ф.

Донецкий физико-технических институт НАН Украины

metlov@host.dipt.donetsk.ua

Методом молекулярной динамики проведены численные эксперименты по долговременной эволюции различных типов начальных сигналов в нелинейных цепочках с реалистическим межатомным потенциалом Exp-6, а также со степенными потенциалами. Найдено, что в тепловом равновесии система характеризуется конечным числом долгоживущих солитоноподобных возмущений, причем между процессами их роста и распада устанавливается динамическое равновесие

SOLITONS IN THE PICTURE OF THERMODYNAMICAL EQUILIBRIUM OF

NONLINEAR CHAINS

Eremeichenkova Yu.V., Metlov L.S., Morozov A.F.

Molecular dynamic numerical simulations are performed to investigate a long-time evolution of different type initial signals in nonlinear chains with realistic Exp-6 potential and with powers ones. It is found that in thermodynamical equilibrium there is a finite number of long-lifetime soliton-like excitations in the system, with dynamical equilibrium being between the processes of their growing and decaying.

Введение. При исследовании колебательного движения атомов в системах при высоких температурах становится актуальным выход за рамки гармонического приближения. Традиционно ангармонизмы учитываются путем включения в межатомный потенциал высших степеней смещений атомов из положений равновесия. Простейшим видом потенциала является учет 3-й и 4-й степеней (потенциалы 2-4 [1-4] и 2-3-4 [5,6]). Также существует ряд работ по реалистическим потенциалам, напр. [6,7].

В [1-7] исследуется (аналитически и методом молекулярной динамики) распад p-сигнала в нелинейных моноатомных цепочках. Это √ гармоника с волновым вектором k=p/a и частотой, лежащей на верхней границе фононного спектра. Смещения атомов в p-сигнале имеют вид

u_n(t) = А (-1)ⁿ cos(wt). (1)

Периодичность по времени исходного сигнала подсказала выбор приближения для поиска аналитических решений нелинейных уравнений движения атомов. В [1-7] использовалось так называемое ⌠rotating wave approximation■ √ RWA, в котором

решение ищется в виде, периодическом во времени

u_n = x_n(t) exp(-iwt) + с.с. (2)

где x_n(t) √функция, медленно меняющаяся во времени (не периодическая). Затем исходная система уравнений линеаризуется по множителю exp(-iwt). Таким образом, почти вся зависимость от времени сосредоточена в периодическом множителе

Солионоподобные решения впервые были аналитически предсказаны (и обнаружены путем численного эксперимента) в [1] в цепочке с потенциалом 2-4 в пределе сильной ангармоничности. Это √ бризеры (другое название - внутренние

локализованные моды). Смещения атомов в бризерах имеют вид

x_n(t) = А(┘ , 0, -½, 1, -½, 0, ...) и x_n(t) = А( ┘ , 0, -1, 1, 0, ┘ )

для четных и нечетных бризеров соответственно.

Бризеры обладают следующими свойствами [3-4]

╖ Образуются в результате амплитудной модуляционной неустойчивости (p-сигнала).

╖ Их частоты всегда выше частоты гармонического p-сигнала.

╖ Их скорости на порядок меньше гармонической скорости звука.

╖ Распадаются необратимо с установлением теплового равновесия.

В [5,6] исследовались существование и устойчивость бризеров в цепочках с потенциалом 2-3-4 (а в [6] - и в реалистических потенциалах Леннарда-Джонса и Морзе). В [6] показано, что добавление малой кубической поправки в потенциал 2-4 практически не влияет на распад p-сигнала и образование бризеров. Однако увеличение кубического слагаемого стабилизирует p-сигнал. При дальнейшем увеличении меняется тип неустойчивости √ появляется ╚удваивающая период неустойчивость╩. На исходный сигнал накладывается быстро растущее возмущение с периодом, вдвое большим периода невозмущенного сигнала. Новый тип неустойчивости не приводит к образованию бризеров, а сразу ведет к тепловому равновесию. В цепочках с реалистическими потенциалами удваивающая период неустойчивость является единственным типом нестабильности, и бризеры в них не образуются [6].

Таким образом, в [1-7] исследовались процессы, приводящие к установлению теплового равновесия в системе. Это √ либо распад p-сигнала на бризеры (а затем распад самих бризеров), либо распад p-сигнала, минуя стадию бризеров. Процессы, происходящие в системе после установления теплового равновесия в системе, и возможность существования там солитонов не исследовались.

Целью настоящей работы является исследование поведения нелинейной системы после установления теплового равновесия.

Методы и приближения. Решались точные уравнения движения атомов

m = - ╤/╤r_i [ ½ S_ij V(x_ij) ]. (3)

в цепочке из 100 частиц с периодическими граничными условиями в приближении ближайших соседей (учет шести координационных сфер дал аналогичные результаты).

Расчет выполнялся в системе единиц, в которой энергия измеряется в [K], масса √ в [а.е.м.], расстояние - в единицах равновесного межатомного расстояния [d₀]. Единица измерения времени равна периоду гармонического p-сигнала Т₀=8.3716×10^-13с (соответствует случаю неона с массой атома m=20.18 а.е.м.).

Для численного решения уравнений (3) применялся алгоритм Йошиды шестого порядка [8]. Шаг дискретизации по времени равен t=0.008Т₀, что дает сохранение энергии с точностью до 10^-4 % в течение всего численного эксперимента (t=10⁵ Т₀).

Использовался реалистический межатомный потенциал Exp-6

V^exp-6(r_ij) = A₀ exp(-a(x_ij √ 1)) - aA₀/6 x_ij^-6; x_ij=r_ij/d₀. (4)

Параметры A₀ = 35.9335 К, a = 13.6519, d₀ = 3.091 Å соответствуют случаю димера неона. Они определялись следующим образом. Отталкивающая часть потенциала рассчитывалась из первых принципов в приближении Хартри-Фока в базисе атомных орбиталей, точно (по Левдину) ортогонализованных на разных узлах [9] и аппроксимировалась экспоненциальной зависимостью от межатомного расстояния. Единственный эмпирический параметр d₀ находился из условия равенства расчетного межатомного расстояния в димере неона с экспериментальным [10].

Для исследования роли различных порядков ангармоничности при движении атомов проводились численные эксперименты по цепочкам со степенными потенциалами. Они определялись как результаты разложения потенциала Exp-6 по

степеням отклонений атомов из положений равновесия

V^exp-6(r_ij) = V₀ + K₂/2 (x_ij;- 1)² + K₃/3 (x_ij;- 1)³ + K₄/4 (x_ij;- 1)⁴ + ...., (5)

Накладывались три вида начальных условий путем задания скоростей атомов V₀

╖ p-сигнал. V₀=3 [(К/а.е.м.)^1/2].

╖ Ударные волны. Моделировались заданием шести атомам (трем с одного конца цепочки, трем √ с другого) начальных скоростей, равных по модулю и направленных внутрь цепочки (V₀=12.25 [(К/а.е.м.)^1/2]).

╖ Белый шум. Моделировался заданием случайных начальных скоростей.

Во всех трех случаях в систему закачивалась одна и та же кинетическая энергия, равная 90 К/атом, что вдвое превышает энергию связи димера неона. Это соответствует сжатому кристаллу в условиях реального эксперимента.

Результаты. p-сигнал. При t╩50Т₀ p-сигнал распадается под действием численного шума (вызванного погрешностью счета) через удваивающую период неустойчивость. С течением времени движение атомов все более хаотизируется. Одновременно идет обратный процесс √ пространственная концентрация энергии, а при t╩600Т₀ образуются хорошо локализованные в пространстве солитоны.

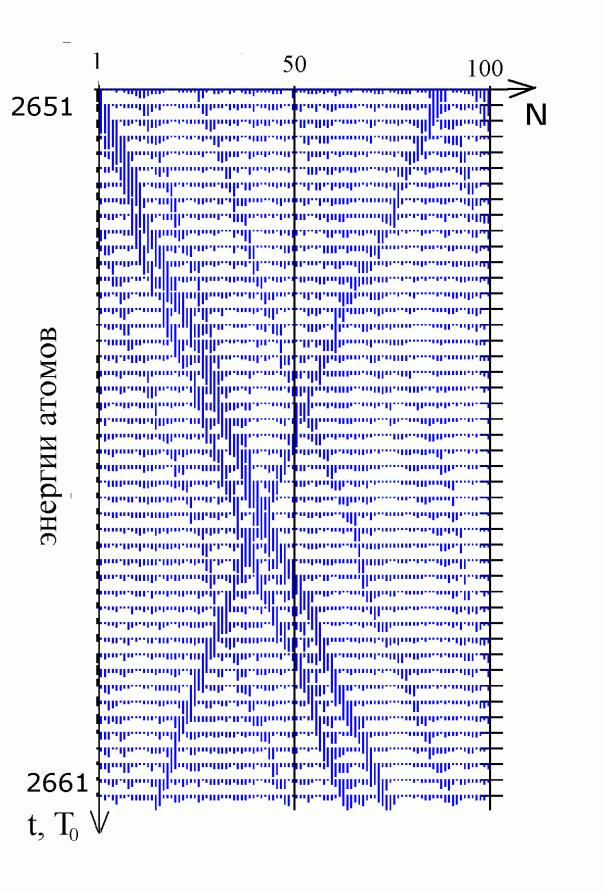
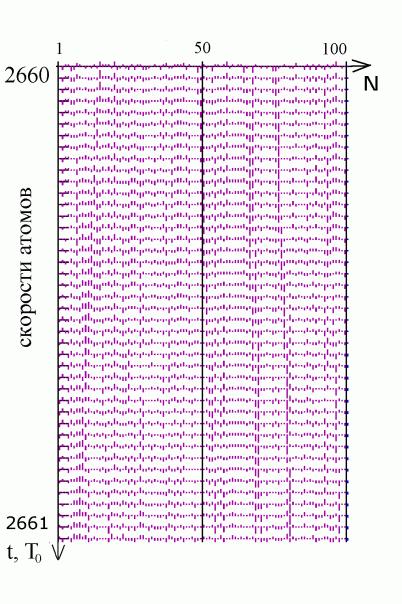
На рис.1 приведен один из моментов, когда в солитонах сконцентрирована наибольшая энергия. Даны диаграммы энергий атомов в последовательные моменты времени. Энергии показаны короткими вертикальными линиями с длиной, пропорциональной величине энергии (положительное направление √ вниз). Форма солитонов дана на рис.2 (увеличенная нижняя часть рис.1). Даны диаграммы скоростей (рис.2а) и энергий (рис.2б). Скорости также показаны короткими вертикальными линиями. Видно, что внутри солитона несколько атомов движутся в одну и ту же сторону, передавая свой импульс впереди покоящимся соседям (как в ударной волне).

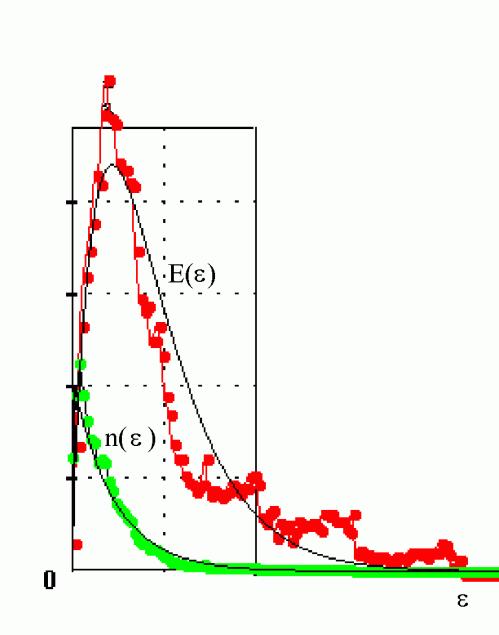
На рис.3 дано распределение атомов по энергиям n(e) (нижний график). Оно определяется так, что величина dn(e)=n(e)de имеет смысл числа атомов, чьи энергии лежат в интервале (e, e+de). Верхний график - распределение Е(e)=en(e), имеющее смысл суммарной энергии атомов, лежащих в энергетическом интервале (e, e+de). Сплошные кривые n(e) и Е(e) соответствуют стандартному распределению Гиббса, полученному в предположении о хаотическом движении атомов в цепочке. Кружками обозначены распределения n(e) и Е(e), найденные в численном эксперименте.

Упорядоченному движению атомов в солитонах соответствуют локальные максимумы на графике Е(e) при энергиях, в 5-8 раз больших средней энергии атома в системе. Согласие ╚экспериментального╩ распределения Е(e) с гиббсовским в области малых e говорит о том, что атомы, не входящие в солитоны, движутся хаотически.

Солитоны, полученные при распаде p-сигнала, обладают свойствами:

1. Слабо взаимодействую друг с другом.

2. По форме аналогичны ударным волнам.

3. Являются однопараметрическими солитонами. Параметр √ скорость v=2-2.3v_s в зависимости от амплитуды (v_s=12.72(K/а.е.м)^1/2√ гармоническая скорость звука).

4. Перемещаясь по цепочке, каждый солитон набирает энергию, а затем ее теряет, расплываясь в пространстве. Между процессами набора энергии и распада устанавливается динамическое равновесие, так что в системе всегда имеется конечное число высокоэнергетических солитонов.

5. За время, пока солитон имеет наибольшую энергию, он успевает пройти 2000-3000 постоянных решетки

6. Периоды времени, когда в солитонах сконцентрирована наибольшая энергия, чередуются с периодами, когда солитоны относительно слабы, а распределение атомов по энергиям согласуется с гиббсовским. Это свойство имеет место также для нелинейных цепочек с потенциалом взаимодействия Леннарда-Джонса [11].

Численные эксперименты по эволюции p-сигнала с энергиями исходного сигнала 300К/атом и 1000К/атом показали, что количество солитонов практически не

Рис.1. Диаграммы энергий атомов.

Рис.2. Диаграммы скоростей (а) и энергий (б) атомов.

Рис.3. Распределения атомов по энергиям.

меняется с ростом энергии. Энергия, накапливаемая в каждом солитоне, растет, однако отношение этой энергии к средней энергии атома в цепочке не меняется.

Ударные волны. Сразу же после начала численного эксперимента каждая исходная волна, охватывающая три атома, распалась на три ударных волны, движущихся со скоростями v~4.5¸5v_s. В каждой из волн в соударениях участвуют по два атома √ один передает весь свой импульс впереди лежащему, покоящемуся, и т.д.

С течением времени (t ╩ 1100 Т₀) ударные волны расплываются в пространстве (в соударениях уже участвуют по 3-5 атомов, движущихся в одном направлении). Они теряют энергию и превращаются в однопараметрические солитоны, аналогичные по форме и свойствам солитонам, полученным при распаде p-сигнала. При t╩2000 Т₀ наступает хаотизация движения атомов в цепочке, ╚экспериментальное╩ распределение Е(e) согласуется с гиббсовским. Затем вновь образуются однопараметрические солитоны со свойствами 1-6.

Таким образом, ударные волны являются предельно локализованной в пространстве (и поэтому неустойчивой) версией однопараметрических солитонов, наблюдаемых при распаде p-сигнала.

Белый шум. После распада любого упорядоченного сигнала и перед образованием однопараметрических солитонов существует стадия хаотического движения атомов. Поэтому для исследования процесса образования солитонов целесообразно использовать в качестве начального условия белый шум

В начале численного эксперимента атомы движутся хаотически, однако распределение Е(e) еще отличается от гиббсовского. Сразу же начинается процесс локализации энергии. При t=80 Т₀ распределение Е(e) выходит на гиббсовское. При t=400Т₀ образуются однопараметрические солитоны, хорошо локализованные в пространстве. Их свойства идентичны свойствам 1-6 солитонов, полученным при распаде p-сигнала и ударных волн.

Таким образом, для образования однопараметрических солитонов не требуется специального вида начального сигнала. Независимо от вида начальных условий, нелинейная цепочка с реалистическим потенциалом Exp-6 приходит в одно и то же стационарное состояние, в котором все величины, усредненные за достаточно большой промежуток времени, постоянны. Оно характеризуется наличием конечного числа долгоживущих высокоэнергетических солитоноподобных возмущений.

Степенные потенциалы. p-сигнал. Рассматривались следующие ситуации.

╖ Потенциалы 2-4 и 2-3-4. p-сигнал распадается через модуляционную неустойчивость на бризеры, аналогичные полученным в [1-6]. В цепочке с потенциалом 2-4 время жизни бризеров составило 120 Т₀ (в потенциале 2-3-4 - 50Т₀). После распада бризеров движение атомов хаотизируется, распределение Е(e) выходит на гиббсовское. Затем в цепочке образуются однопараметрические солитоны со свойствами 2-6. Однако эти солитоны живут очень недолго (╩50 Т₀), успевая за это время пройти цепочку из 100 атомов 3-4 раза. Столь короткое время жизни обусловлено тем, что в цепочке с потенциалами 2-4 и 2-3-4 солитоны намного сильнее взаимодействуют друг с другом.

╖ Потенциалы 2-3-4-5-6 и 2-3-4-5-6-7-8. p-сигнал стабилен.

╖ Потенциал 2-3-4-5-6-7-8-9-10. p-сигнал распадается через удваивающую период неустойчивость. Образуются однопараметрические солитоны со свойствами 1-6 (слабо взаимодействующие друг с другом и имеющие большие времена жизни).

Таким образом, добавление кубической ангармоничности дает в картине распада p сигнала и образования солитонов лишь количественные изменения по сравнению с потенциалом 2-4. Учет 5-6 и 7-8 порядков стабилизирует p сигнал. При учете 9-10 степеней происходит смена типа неустойчивости, а свойства солитонов полностью совпадают со свойствами солитонов, полученных в цепочках с полным потенциалом Exp-6. Таким образом, малые в количественном отношении поправки дают качественное изменение поведения атомов. Чтобы избежать подобных осложнений в реальных кристаллах, необходимо использование реалистических межатомных потенциалов.

Выводы. В настоящей работе исследовано поведение нелинейной системы в состоянии термодинамического равновесия. Обнаружены солитоны, по свойствам сильно отличающиеся от бризерв √ единственных солитонов (кроме темных солитонов [1]), на сегодняшний день предсказанных и наблюдавшихся в численном эксперименте в дискретных цепочках.

Отличия в свойствах следующие.

╖ Бризеры характеризуются двумя параметрами √ частотой и скоростью. В однопараметрических солитонах нет периодичности во времени, единственный параметр - скорость.

╖ Скорость бризера √ дозвуковая и на порядок меньше скорости однопараметрического солитона (сверхзвуковой).

╖ В бризере соседние атомы движутся в противофазе. В однопараметрическом солитоне несколько соседих атомов движутся в одном направлении. Поэтому в бризере накапливается большая энергия, чем в однопараметрическим солитоне.

╖ Бризеры образуются в специальных условиях √ только в потенциалах 2-4 и 2-3-4 при распаде p-сигнала. Однопараметрические солитоны образуются как в степенных, так и в реалистических потенциалах, причем самопроизвольно, из хаотического движения атомов.

╖ Бризеры имеют малое время жизни и распадаются необратимо. Для однопараметрических солитонов между процессами образования и распада устанавливается динамическое равновесие.

Таким образом, в состоянии теплового равновесия нелинейная цепочка характеризуется наличием конечного числа долгоживущих высокоэнергетических возмущений. Можно ожидать, что подобные возмущения могут существовать в трехмерном случае и давать заметное увеличение теплопроводности кристалла при высоких температурах, а также влиять на длительную прочность твердых тел.

Литература

1. А.С.Долгов ФТТ 28, 1641 (1986).

2. V.M.Burlakov, S.A.Kiselev, V.I.Rupasov Phys.Lett.A 147, 130 (1990).

3. K.W.Sandusky, J.B.Page, K.E.Shmidt Phys.Rev.B 46, 6161 (1992).

4. T.Cretegny, T.Dauxois, S.Ruffo, A.Torchini Physica D 121, 109 (1998).

5. S.R.Bichham, S.A.Kiselev, A.J.Sievers Phys.Rev.B 47, 14206 (1993).

6. K.W.Sandusky, J.B.Page Phys.Rev.B 50, 866 (1994).

7. T.Rossler, J.B.Page Phys.Lett.A 204, 418 (1995).

8. H.Yoshida Phys.Lett.A 150, 262 (1990).

9. Ю.В.Еремейченкова Теория энергетической структуры изоляторов при сверхвысоких давлениях: Автореф. дисс. к. ф.-м. н.-Донецк, 1999.-139 с.

10. J.F.Ogilvie, F.J.Wang, J. Mol. Struct. 273, 277 (1992).

11. L.S.Metlov ФТВД, 11, 3, 121 (2001).

Подписи к рисункам

Рис.1. Диаграммы энергий атомов.

Рис.2. Диаграммы скоростей (а) и энергий (б) атомов.

Рис.3. Распределения атомов по энергиям.